What are you having difficulty with in Cimg.h? I don’t know C++ but it looks like the functions simply build on each other incrementally and there is many versions of a general function to cover all the bases. When we script in G’MIC it is easier to organize the way we want it because things are mostly in one place under a command.
Basically reading how it works
I only get a few part of this:
if (!std::strncmp(ss,"sort(",5)) { // Sort vector
_cimg_mp_op("Function 'sort()'");
s1 = ss5; while (s1<se1 && (*s1!=',' || level[s1 - expr._data]!=clevel1)) ++s1;
arg1 = compile(ss5,s1,depth1,0,bloc_flags);
arg2 = arg4 = 1; arg3 = ~0U;
if (s1<se1) {
s0 = ++s1; while (s0<se1 && (*s0!=',' || level[s0 - expr._data]!=clevel1)) ++s0;
arg2 = compile(s1,s0,depth1,0,bloc_flags);
if (s0<se1) {
s1 = ++s0; while (s1<se1 && (*s1!=',' || level[s1 - expr._data]!=clevel1)) ++s1;
arg3 = compile(s0,s1,depth1,0,bloc_flags);
arg4 = s1<se1?compile(++s1,se1,depth1,0,bloc_flags):1;
}
}
_cimg_mp_check_type(arg1,1,2,0);
_cimg_mp_check_type(arg2,2,1,0);
if (arg3!=~0U) _cimg_mp_check_type(arg3,3,1,0);
_cimg_mp_check_type(arg4,4,1,0);
p1 = _cimg_mp_size(arg1);
pos = vector(p1);
CImg<ulongT>::vector((ulongT)mp_sort,pos,arg1,p1,arg2,arg3,arg4).move_to(code);
return_new_comp = true;
_cimg_mp_return(pos);
}
What I think I get:
- $n seem to be relative to arg_n.
- cimg_mp_check_type seem to define defaults. I guess that.
- CImg::vector((ulongT)mp_sort… This is where the sorting comes in.
It’s everything else I don’t get.
That being said, I resorted to looking at geeksforgeeks, and using iterative quicksort in hope of being able to sort vector using values from another vector. Kind of like [8,5,1,2] using [3,0,2,1] as sort reference would result in [5,2,1,8].
The ideal would be having something like sort as it is in current state now, but with an extra parameter being a vector as reference.
My thoughts (I may be wrong…): Where is $n? I can’t find it… Type defines argument type. Cimg defines the function and the input, arguments and output it takes.
!std::strncmp(ss,"sort(",5)
controls how many arguments it is allowed to take. This Cimg function translates to the math intepreter’s sort().
I’m saying $n is linked to argn.
That being said, I found my solution for sorting an array with another array, it’s not ideal:
rep_test:
eval "begin(
partition(lo,ho)=(
vi=vb[ho];
ni=(lo-1);
for(p=lo,p<=ho-1,++p,
if(vb[p]<=vi,
++ni;
swap(va[ni],va[p]);
swap(vb[ni],vb[p]);
);
);
swap(va[ni+1],va[ho]);
swap(vb[ni+1],vb[ho]);
ni+1;
);
quicksort_iterative(low,high)=(
top=-1;
stack[++top]=low;
stack[++top]=high;
while(top>=0,
ho=stack[top--];
lo=stack[top--];
p=partition(lo,ho);
if(p-1>1,
stack[++top]=lo;
stack[++top]=p-1;
);
if(p+1<ho,
stack[++top]=p+1;
stack[++top]=ho;
);
);
);
);
stack=vector(#4,0);
va=[8,5,1,2];
vb=[3,0,1,2];
print(va);
print(vb);
quicksort_iterative(0,3);
print(va);
print(vb);"
Yields:
C:\Windows\System32>gmic rep_test
[gmic]-0./ Start G'MIC interpreter.
[gmic_math_parser] va = (uninitialized) (compiled as 'vector4', memslot = 39)
[gmic_math_parser] vb = (uninitialized) (compiled as 'vector4', memslot = 44)
[gmic_math_parser] va = (uninitialized) (compiled as 'vector4', memslot = 39)
[gmic_math_parser] vb = (uninitialized) (compiled as 'vector4', memslot = 44)
[gmic_math_parser] va = [ 8,5,1,2 ] (size: 4)
[gmic_math_parser] vb = [ 3,0,1,2 ] (size: 4)
[gmic_math_parser] va = [ 5,1,2,8 ] (size: 4)
[gmic_math_parser] vb = [ 0,1,2,3 ] (size: 4)
[gmic]-0./ End G'MIC interpreter.
Nope… Something’s wrong, but closer to the answer. The second va should be [5,1,2,8].
EDIT: I had to add a 'swap(va[ni+1],va[ho]);' above the 'swap(vb[ni...]);'. Now it works.
It looks a lot cleaner than your previous attempt. I can actually read it. 

I tested it more, it’s way too slow for much larger use. In comparison with current sort, that is. Wouldn’t matter much for 255 arrays or less though.
Yeah, you would have to understand CImg. Hope you do because you have lots of ideas that would benefit from compilation.
Now, I have a new question. Can it be possible for sort to be modified to have option to return the index number? I think that may be the easiest fix. This would not require two vectors at all, and can be easily be utilized with fill to return a vector sorted by values of another vector instead of itself.
The function sort(X,_is_increasing,_nb_elts,_size_elt) has an argument size_elt that gives the number of size of each array element, seen as a sequence of values.
For instance, that means each array element can be defined by two values : value,ind, and you can sort this according to value (the first value of each element).
foo :
eval "
arr = [ 3,0,
6,1,
2,2,
0,3 ];
sort_arr = sort(arr,1,4,2);
print(sort_arr);
"
gives you:
[gmic_math_parser] sort_arr = [ 0,3,2,2,3,0,6,1 ] (size: 8)
This means for each sorted value, you can associate an index (or any other value).
Here’s one I’ve been wondering about since doing stuff with pyramid methods:
What’s the most efficient way to solve the asymmetric upscale vs downscale of bilinear/bicubic scaling in g’mic?
In g’mic, x-axis pixel coords with bilinear or bicubic interp range from 0 to (w-1), where 0 is the centre of the first pixel and (w-1) the centre of the last. That effectively means the leftmost image extent is at -0.5, and the rightmost at (w-0.5).
OK, so why could that present a problem? If you upscale by a fairly large ratio then back down again, you will find the image is “zoomed in” compared to the original. Some information at the edges was lost!
One way around it is to use warp for upscaling, fixing the coords by calculation. But is there a better/faster way? I feel like I’m missing something really obvious… anyone got some ideas?
I asked @Iain about pyramids a while back. He showed me he calculates the required minimum edge and then interpolates it so that the pyramiding works out. My issue with pyramids is that the resizing alone seems to disrupt any good it does, i.e., output from pyramids is worse than single scale. Perhaps, I am just doing it wrong…
@garagecoder It would be nice if you shared some of your code, with pretty pictures, to demonstrate your issue. 
Maybe add a 1px edge before downscaling, and crop the result ?
You’re right about examples, I’ll do that properly tomorrow hopefully. For pyramid methods I tend to use convolution because the scales are fixed, I only mention it because that’s where I started paying attention to differences in scaling methods.
@David_Tschumperle I guess what I’m looking for is a precise yet fast way to match bilinear/bicubic upscale to the box average downscale in a way which avoids any pixel shifts whatsoever. In other words, correct pixel centre alignment rather than approximate.
Here is a toy example workaround (hopefully I got the maths right):
gcd_resize_bl : skip ${2=100%},${3=100%}
foreach {
$1,$2,$3,3,"[w#0*(x+0.5)/w-0.5,h#0*(y+0.5)/h-0.5,d#0*(z+0.5)/d-0.5]"
warp.. .,0 rm.
}
One thing I do is resize dimensions by 1/3 for my pyramids. This means if you downsize and then upsize, you can keep pixel alignment, because odd-sized blocks have a definite middle point.
Some extra steps are required to make it work. The full sized image needs to have dimensions that are multiples of 3. And when I upsize, I do this
resize[0] {(w*3)-2},{(h*3)-2},{d},{s},5,0
resize[0] {w+2},{h+2},{d},{s},0,1,0.5,0.5
So the pixels are aligned properly.
As promised, some pictorial expansion on the problem…
Starting from a 128x128 image, resize by a factor of 10 with bilinear, then back down again (using box average):

Why does it happen? Simply put, the centres of the sample points don’t match. In g’mic, bilinear uses one scheme and downscale (box average) uses another. Below is an enlarged two “pixel” image, showing sample points used when scaling to 4 pixels.
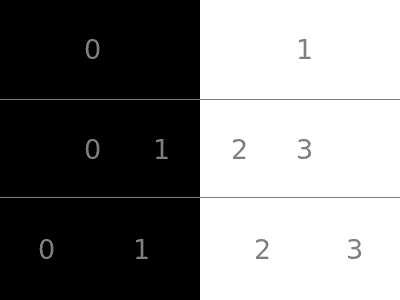
From the top: original, g’mic bilinear, matched to g’mic downscale. The scheme which matches downscale is also commonly used by graphics cards.
And resulting values from scaling a two pixel image to 4:
gmic "(0,1)" r 4,1,1,1,3 # (0,0.333333,0.666667,1)
gmic "(0,1)" gcd_resize_bl 4 # (0,0.25,0.75,1)
Still on the topic of scaling, one I don’t fully understand. For this one, we need the above gcd_resize_bl and a version of laplacian with periodic boundary:
gcd_laplacian : foreach g xy,1,2 g.. x,-1,2 g. y,-1,2 add done
The idea is to scale the laplacian, then recover the original with ilaplacian:
gcd_laplacian gcd_resize_bl 400%,400% ilaplacian 0 n 0,255
From the top: original, laplacian upscale, bicubic upscale

It works! But there are questions… is this equivalent to a b-spline? Is there another way of doing it which is faster? Can we recover the colours too?
Edit: I suppose it’s equivalent to resize nearest neighbor then gaussian blur?
I never use ilaplacian because of the colour/contrast cast. Do you a way to combat that?
Does separating channels and process with ilaplacian work?
It’s mostly about the boundary handling - a general rule is to use it with periodic boundary commands. If you try the gcd_laplacian with ilaplacian 0 you’ll find the reversal is close to perfect, but you do need to save and restore the average channels vector. An example “null op”:
gcd_laplacian_roundtrip :
+r 1,1,1,100%,2 # keep the vector average
l[0] { g xy,1,2 g.. x,-1,2 g. y,-1,2 add } # periodic laplacian
# manipulate the laplacian here...
ilaplacian[0] 0 # invert the laplacian
repeat s#0 { sh[0] $> add. {i[#1,$>]} rm. } # restore the average vector
@Reptorian I worked out what to do: the ilaplacian output values range is tied to the number of pixels. If you multiply by the ratio of (original whds / resized whds) then you can add back the average vector as normal (see above).
Note that you can also manipulate the 1st derivative (gradient), then take the divergence of that to get to a laplacian, which is sometimes more stable:
g xy,1,2 # periodic gradient
# do some stuff to the gradient here...
g.. x,-1,2 g. y,-1,2 add # sum of gradients (of gradients) = laplacian
@David_Tschumperle: Your suggestion of argmin works for the most part. But it seems to ignore colors where closest match don’t exist. I’d like a solution to that. Details below, and I left a comment near begin(); where the problem is caused by. I even made some codes to try to address that problem, but they did not work as you can see in the code below.
The line that needs to be edited is:
p=argmin(sqrt(color_sum)); # Is there any alternative to this?
It seems that now I am closer to making the G’MIC version of index though with color restriction in mind, and windows. Unlike the default G’MIC index, it uses Jarvis, Judice, and Ninke dithering method.
Here’s proof:
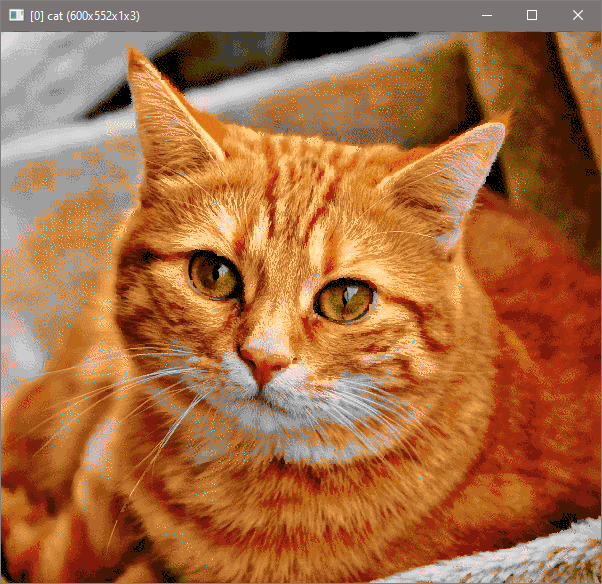
However, I am having this artifact:
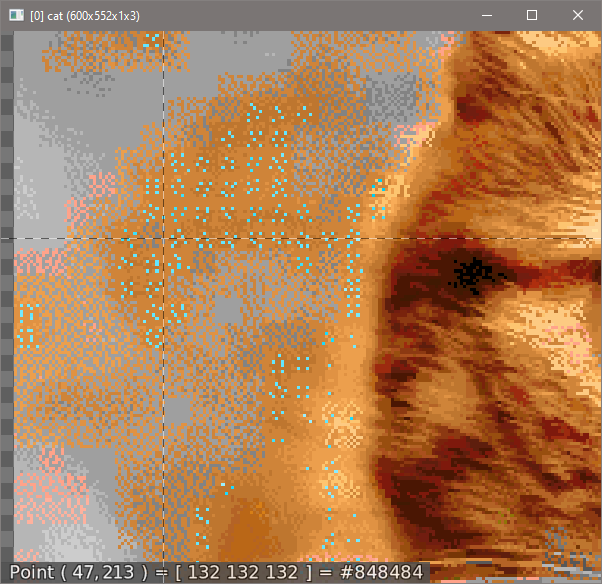
Those blue colors are not suppose to be there.
rep_index_by_window_and_color_restriction
$ sp cat +pal amiga7800mess rep_index_by_window_and_color_restriction[0] [1],1,6,8,8,1,1 rm.
#@cli rep_index_by_window_and_color_restriction:[palette],0<=_dithering<=1,_color_restriction>2,_window_width,_window_height,_window_depth,_map_palette={ 0 | 1 }
#@cli : Index images per window
rep_index_by_window_and_color_restriction:
dithering,col_res,wi_w,wi_h,wi_d,map_palette,timg={cut($2,0,1)},{cut(int(abs($3)),2,w#-1)},{vmax(vector(#3,1),int(abs([${4-6}])))},{$7%2},{$!}
pass$1 1
if h#-1>1&&d#-1==1
rm. pass$1 0
rotate. -90
elif h#-1>1&&d#-1>1
rm. pass$1 0
colormap. 0,,0
fi
if $dithering
# Jarvis, Judice, and Ninke Dithering Array
jjn_1R0D,jjn_2R0D,\
jjn_2L1D,jjn_1L1D,jjn_M01D,jjn_1R1D,jjn_2R1D,\
jjn_2L2D,jjn_1L2D,jjn_M02D,jjn_1R2D,jjn_2R2D\
={([7,5,3,5,7,5,3,1,3,5,3,1]/48)*$dithering}
fi
eval "
const spectrum_size=s#-1;
const rf=$timg;
valid_spec=1;
repeat(rf,id,
if(s#id!=spectrum_size,valid_spec=0;break(););
);
valid_spec;
"
if !${} error incompatible_img_pal fi
if $col_res==w#-1
index[^-1] [-1],$dithering,$map_palette
rm.
return
fi
repeat $timg local[$>,-1]
{
ow,oh,od,tw,th,td,nw,nh,nd={od=[w#0,h#0,d#0];wd=[$wi_w,$wi_h,$wi_d];td=ceil(od/wd);nd=td*wd;[od,td,nd]}
r[0] $nw,$nh,$nd,100%,0,3,.5,.5,.5
$tw,$th,$td,1,*"begin(
const nb_cols=w#-1;
const spectrum_size=s#1;
const inc_spectrum_size=spectrum_size+1;
const nb_restrict=$col_res;
const dec_nb_restrict=nb_restrict-1;
const res_y_spec=nb_restrict*spectrum_size;
const wi_w=$wi_w;
const wi_h=$wi_h;
const wi_d=$wi_d;
const dec_wi_w=wi_w-1;
const dec_wi_h=wi_h-1;
const dec_wi_d=wi_d-1;
const box_dim=wi_w*wi_h*wi_d*spectrum_size;
init_freq_y_ind=expr('(x%2)?int(x/2);',nb_cols*2);
init_sel_res_pal_dist_arr=vector(#nb_restrict,0);
$dithering?(
# jjn_1R0D jjn_2R0D
# jjn_2L1D jjn_1L1D jjn_M01D jjn_1R1D jjn_2R1D
# jjn_2L2D jjn_1L2D jjn_M02D jjn_1R2D jjn_2R2D
const jjn_1R0D=$jjn_1R0D;
const jjn_2R0D=$jjn_2R0D;
const jjn_2L1D=$jjn_2L1D;
const jjn_1L1D=$jjn_1L1D;
const jjn_M01D=$jjn_M01D;
const jjn_1R1D=$jjn_1R1D;
const jjn_2R1D=$jjn_2R1D;
const jjn_2L2D=$jjn_2L2D;
const jjn_1L2D=$jjn_1L2D;
const jjn_M02D=$jjn_M02D;
const jjn_1R2D=$jjn_1R2D;
const jjn_2R2D=$jjn_2R2D;
);
);
c_xp=x*wi_w;
c_yp=y*wi_h;
c_zp=z*wi_d;
freq_y_ind=init_freq_y_ind;
repeat(wi_d,oz,
pos_z=c_zp+oz;
repeat(wi_h,oy,
pos_y=c_yp+oy;
repeat(wi_w,ox,
pos_x=c_xp+ox;
v_col=I(#0,pos_x,pos_y,pos_z);
color_sum=vector(#nb_cols,0);
repeat(spectrum_size,k,
color_sum+=sqr(crop(#1,0,0,0,k,nb_cols,1,1,1)-v_col[k]);
);
# color_sum=sqrt(color_sum);
# repeat(nb_cols,ins_dist,
# freq_y_ind[ins_dist*2]=color_sum[ins_dist];
# );
p=argmin(sqrt(color_sum)); # Is there any alternative to this?
++freq_y_ind[p*2];
);
);
);
freq_y_ind=sort(freq_y_ind,0,nb_cols,2);
res_col_id=(freq_y_ind)[1,nb_restrict,2];
res_pal=vector(#res_y_spec,0);
repeat(nb_restrict,p,
res_pal_col=I(#1,res_col_id[p],0,0);
repeat(spectrum_size,q,
res_pal[q*nb_restrict+p]=res_pal_col[q];
);
);
min_out_of_boundary_offset_pos=[c_xp,c_xp,c_yp]+[-1,wi_w,wi_h];
repeat(wi_d,oz,
pos_z=c_zp+oz;
repeat(wi_h,oy,
pos_y=c_yp+oy;
repeat(wi_w,ox,
pos_x=c_xp+ox;
res_color_sum=init_sel_res_pal_dist_arr;
v_col=I(#0,pos_x,pos_y,pos_z);
repeat(spectrum_size,k,
res_color_sum+=sqr((res_pal)[k*nb_restrict,nb_restrict]-v_col[k]);
);
old_color=I(#0,pos_x,pos_y,pos_z);
new_color=I(#1,res_col_id[argmin(sqrt(res_color_sum))],0,0);
I(#0,pos_x,pos_y,pos_z)=new_color;
diff_color=old_color-new_color;
use_strip_1D=(pos_y+1)<min_out_of_boundary_offset_pos[2];
use_strip_2D=(pos_y+2)<min_out_of_boundary_offset_pos[2];
use_strip_1D?(
I(#0,pos_x,pos_y+1,pos_z)+=diff_color*jjn_M01D;
);
use_strip_2D?(
I(#0,pos_x,pos_y+2,pos_z)+=diff_color*jjn_M02D;
);
(pos_x-2)>min_out_of_boundary_offset_pos[0]?(
use_strip_1D?(
I(#0,pos_x-2,pos_y+1,pos_z)+=diff_color*jjn_2L1D;
);
use_strip_2D?(
I(#0,pos_x-2,pos_y+2,pos_z)+=diff_color*jjn_2L2D;
);
);
(pos_x-1)>min_out_of_boundary_offset_pos[0]?(
use_strip_1D?(
I(#0,pos_x-1,pos_y+1,pos_z)+=diff_color*jjn_1L1D;
);
use_strip_2D?(
I(#0,pos_x-1,pos_y+2,pos_z)+=diff_color*jjn_1L2D;
);
);
(pos_x+1)<min_out_of_boundary_offset_pos[1]?(
I(#0,pos_x+1,pos_y,pos_z)+=diff_color*jjn_1R0D;
use_strip_1D?(
I(#0,pos_x+1,pos_y+1,pos_z)+=diff_color*jjn_1R1D;
);
use_strip_2D?(
I(#0,pos_x+1,pos_y+2,pos_z)+=diff_color*jjn_1R2D;
);
);
(pos_x+2)<min_out_of_boundary_offset_pos[1]?(
I(#0,pos_x+2,pos_y,pos_z)+=diff_color*jjn_2R0D;
use_strip_1D?(
I(#0,pos_x+2,pos_y+1,pos_z)+=diff_color*jjn_2R1D;
);
use_strip_2D?(
I(#0,pos_x+2,pos_y+2,pos_z)+=diff_color*jjn_2R2D;
);
);
);
);
);
# if(!x&&!y,
# print(res_pal);
# repeat(spectrum_size,pos,
# print((res_pal)[pos*nb_restrict,nb_restrict]);
# );
# );
"
}
done
With the attempt to get around the problem:
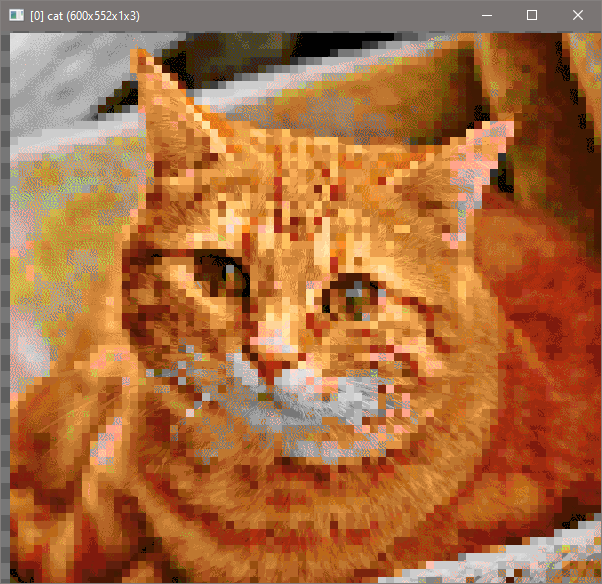
That’s ugly.
EDIT: What I think I could do is to do error-diffusion using temporary channels for use. I guess that will work, but it’s not ideal methinks. Possibly my only solution.
Ah, now I have a theory of how I can do it.
[ 0 - 192 ] => 1
[ 1 - 232 ] => 2
[ 2 - 765 ] => 6
[ 3 - 432 ] => 3
[ 4 - 139 ] => 0
[ 5 - 365 ] => 5
[ 6 - 465 ] => 4
By doing this, I would be able to avoid the need of more channels. I’m not sure how to do this yet though.
EDIT: Oh, now I see what to do for this one.
EDIT: Looks like I have no choice, but to do multi-channel approach as this idea did not work.
EDIT: Multi-channel approach did work. Consider this solved.