This implements an heat transfer partial derivative equations solver, adapted fr…om https://www.researchgate.net/publication/220663968 and originally meant for image inpainting and reconstruction. However, I have found that it doesn't really reconstruct anything unless you apply a large amount of iterations, which is not compatible with dt's "realtime"-ish purpose.
The algorithm is adapted for a wavelets framework, which makes it super slow (OpenCL incoming ASAP) but allows to include spatiality in the parameters. It's very close in logic to the filmic highlights reconstruction. Basically, it allows to make pixels spill (or un-spill) on their neighbours.
The module comes with 4 presets to showcase what it can do, since it's quite close to physics and can be used in a variety of situations:
1. blind deconvolution by gradient descent, following the steepest gradient direction,
2. anisotropic diffusion, or directional blur if you prefer, propagating colors in the perpendicular direction of edges, (so, either
4. joint sharpening and denoising,
5. highlights inpainting (although I'm not convinced by the results).
## Use case 1
The motivation for this module was to spill image colors outside of its borders, as a special effect for prints:

This is achieved by underlaying a framing module, for which I had to remove the iop_order fences in rawoverexposed.c and finalscale.c. This seems to make dt crash sometimes, even though it's hard to know what is responsible for the crashes these days.
## Use case 2
Deblur. For this, the module is put right after exposure. Before/After 1/After 2/After 3 (images at 1:1):




Notice that it respects the depth of field fairly well and does not display halos. The filter is applied on linear RGB so it's really suited to remove non-uniform lens blur.
## Caveats
The module is slow… Not much I can do besides providing an OpenCL kernel. 1 to 2 iterations are ok, up to 4 iterations is meh, more than 4 iterations is something you can do before taking a walk.
## How to use
Read the tooltips and use the presets. Details below.
### General
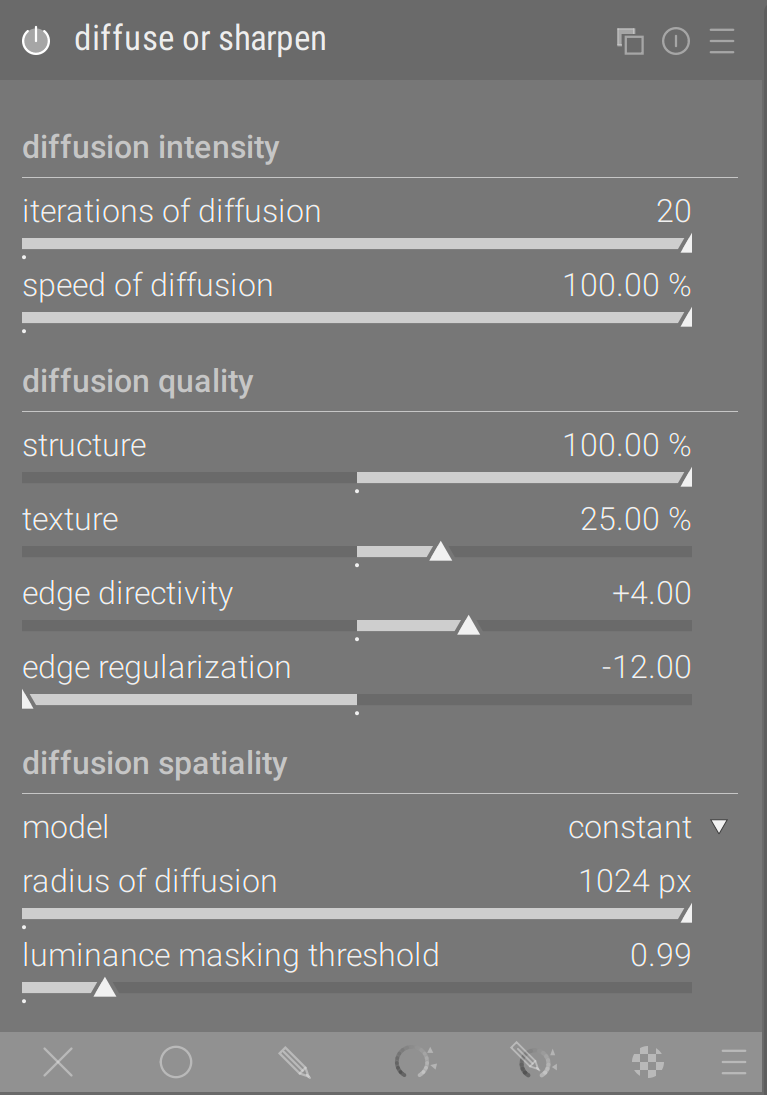
Every order of derivatives comes with 3 sliders:
* strength:
* positive values make that derivative smoother (diffusion),
* negative values make that derivative more oscillatory (sharpening),
* edges directivity:
* high values make the 2D derivatives more directional (anisotropic), following a direction perpendicular to the steepest gradient
* low values makes the 2D derivatives more uniform (isotropic), in a radial direction, more like usual blurs,
* edges regularization:
* high values apply an higher penalty to derivatives of high magnitude, to avoid overshoot and gradient reversals around edges,
* low values apply a lower (or even close to none) penalty to derivatives of high magnitude, allowing stronger effects but also overshoots.
* low magnitude derivatives (zero and close) are never affected by the regularization parameter. The value of the regularization drives the speed of the transition between the low and high magnitude.
Overshoots cause artifacts, such asnoise, gradient reversals (halos, fringes), etc. If they happen, you need to dampen your derivatives (strength and/or regularization).
The speed of diffusion is a general factor applied to all strengths settings at once. As the number of iterations increases, it's a good idea to decrease the speed to avoid issues.
### First order
First order derivatives are linked to simple diffusion, such as hazing and light leaks. Used in sharpening mode, it's very prone to gradients reversals, so don't force on the strength.
### Second order
The second order is isotropic because it is simply the detail layer of the wavelets separation, that uses a B-spline blur. This setting is exactly similar to the luma curve in contrast equalizer, but the wavelets decomposition is applied in linear RGB instead of Lab. Second order derivatives are linked to sharp edges and acutance (local filter), but also to noise.
### Third order
The third order is linked to the smoothness of the second, so it can be used to alleviate noise when the second order is used in sharpening mode.
### Non-local fourth order
The non-local fourth order will increase or decrease the curvature of the second order by sampling points further away. This can be used to inpaint the texture in damaged areas, or smoothen or increase oscillations. Used with large radii (> 128 px), and small strength, it behaves in the same spirit as the local laplacian for local contrast enhancement.
### Spirit
Start with setting the first and second orders roughly, as they yield the more dramatic results, zoomed-out. When you are sort-of pleased with the result, zoom-in and fine-tune with the third order by watching out for noise. Finish with fourth order for non-local effects like increasing the volume of features.
Then finish with the diffusion speed, to boost or temper the correction. For large deblurrings, inpaintings or joint sharpening + denoising, more iterations will be needed with smaller diffusion speed to avoid overshoots. In the literature, such applications need more than 50 iterations.
By combining the weights of each order, you are virtually able to add or remove any kind of diffusion (atmospheric hazing, frosten glass, lens blur, coma, etc.) or even perform edge-aware surface blurs.
While the same method could be used to denoise, it doesn't take advantage of the inter-channels correlations, so it's no better than the usual denoising modules (but could be modified in Y0U0V0 for that purpose).
![]()



