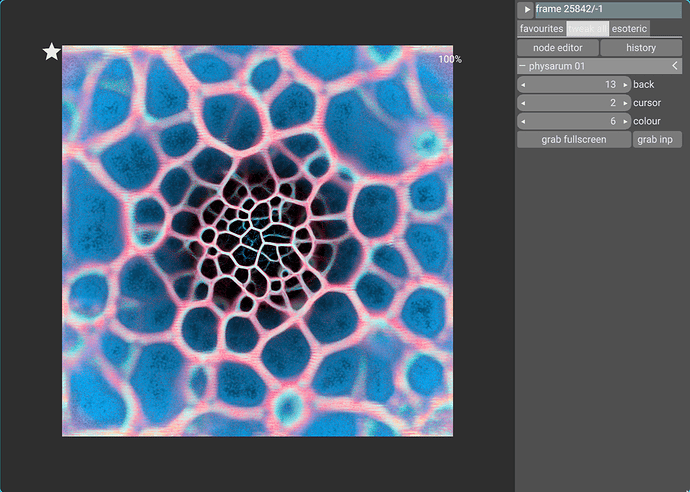
Iteration #5: Doing it in 3D!
As the basic algorithm was quite simple to implement, I wondered if it couldn’t be easily adapted to 3D: instead of drawing pixels in a 2D image, why not draw voxels in a 3D (discrete) image?
In the end, it took a bit more work than expected (as usual!), because to convert the algorithm to 3D, I had to :
- Implement the drawing of 3D Gaussians oriented by any 3D vector (which is definitely harder than doing it in 2D!).
- Adapt the sensor measures in 3D, by scanning at different voxels that belongs to the 3D plane that is orthogonal to each agent’s orientation. I had to do a bit of geometry on paper again (it’s been a long time TBH!).
- Write a code to render the 3D volumetric image (which is dense by definition), as a 3D mesh object that renders ‘nicely’ (I used some rendering + smoothing tricks, thanks G’MIC to already have so many different smoothing algorithms implemented!).
And finally, this is what I get:
It’s not that beautiful, but before all, I wanted to test if the algorithm can be extended to 3D. The answer is yes, and I’ll be able to go to bed tonight having learned something, even if I don’t explore this 3D aspect any further!
This time, that really closes this G’MIC Adventures episode 
foo :
100,100,100 => canvas
100%,100%,100% => trail
40%,40%,40%,6,"[ u(w#$trail - 1),u(h#$trail - 1),u(d#$trail - 1),unitnorm([g,g,g]) ]" => agents
w[canvas] ${"fitscreen [canvas],35%"}
visu_ang=0
nb_orientations=3
sensor_distance=10
sensor_angle=30
motion_distance=3
motion_angle=30
motion_moment=0.7
opacity=0.3
# Define header for math expression.
header="
const no = $nb_orientations;
const sd = $sensor_distance;
const sa = $sensor_angle;
const md = $motion_distance;
const ma = $motion_angle;
const mm = $motion_moment;
const opacity = $opacity;"
# Generate frames.
repeat 400 {
e " - "{_round($%*100)}%
f[canvas] 0
f[agents] :${header}"
draw_gaussian3d(ind,xc,yc,zc,u,v,w,siz,anisotropy,opacity) = (
unref(dg3d_mask,dg3d_one,dg3d_isiz2);
dg3d_vU = [ u,v,w ];
dg3d_vUvUt = mul(dg3d_vU,dg3d_vU,3);
dg3d_T = invert(dg3d_vUvUt + max(0.025,1 - sqrt(anisotropy))*(eye(3) - dg3d_vUvUt));
dg3d_expr = string('T = [',v2s(dg3d_T),']; X = ([ x,y,z ] - siz/2)/siz; exp(-12*dot(X,T*X))');
dg3d_mask = expr(dg3d_expr,siz,siz,siz);
dg3d_one = vector(#size(dg3d_mask),1);
const dg3d_isiz2 = int(siz/2);
draw(#ind,dg3d_one,xc - dg3d_isiz2,yc - dg3d_isiz2,zc - dg3d_isiz2,siz,siz,siz,opacity,dg3d_mask);
);
A = I; X = A[0,3]; U = A[3,3];
# Get sensor measures.
Y = X + sd*U;
V = unitnorm(cross(U,[g,g,g]));
max_value = -inf; max_Z = [ 0,0,0 ];
repeat (no,k,
l = lerp(0,sd*tan(sa°),k/(no - 1));
Z = Y + l*V;
R = rot(U,36°);
repeat (10,a,
value = i(#$trail,Z,1,2);
value>max_value?(max_value = value; max_Z = Z);
Z = Y + R*(Z - Y);
);
);
# Turn agent according to sensor measure.
U = unitnorm(lerp(U,unitnorm(max_Z - X),mm));
# Move agent along new orientation.
X+=md*U;
X[0]%=w#$trail;
X[1]%=h#$trail;
X[2]%=d#$trail;
iX = round(X);
++i(#$trail,iX);
draw_gaussian3d(#$canvas,iX[0],iX[1],iX[2],U[0],U[1],U[2],9,0.8,opacity);
[ X,U ]"
b[trail] 1,2
n[trail] 0,1
+render_in_3d[canvas] $visu_ang on. frame.png,$> rm. visu_ang+=2
if !{*}" || "{*,ESC} break fi
}
k[canvas]
render_in_3d :
foreach {
+ge. 0.1 * * 255 pointcloud3d
s3d +r.. 1,{-2,h/3},1,1 /. 300 j.. . rm.
a y
circles3d 1.5
-3d. 50,50,50 r3d. 1,1,1,75 *3d. 0.5 f3d 1200
r3d. 0,1,0,$1
1024,1024,1,3
*3d.. 15 j3d. ..,50%,50% k.
rolling_guidance. 4,10,0.5
smooth. 100,0.3,1,2,5
n. 0,255 map. hot
rs 50%
w. ${"fitscreen .,35%"}
}
![]()