How to transform a curve into a circle ?

Software G'MIC
21

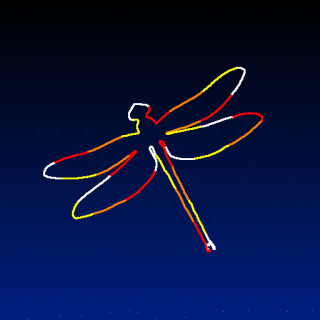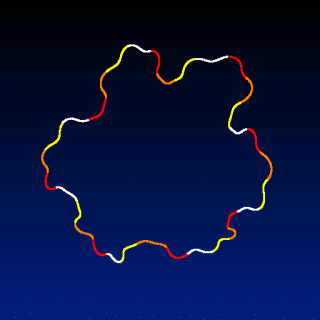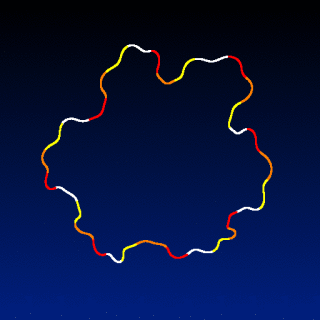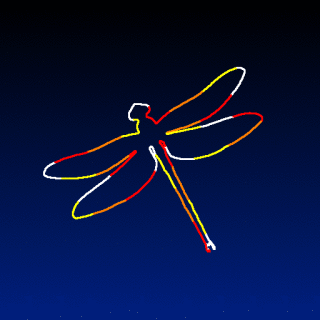
No. Because I used a trick to simulate a Mean-Curvature Flow evolution of the curve points (rendering of the curve as a 2D silhouette + blur + threshold + reparameterization).
The “correct” way would be to stick with the initial curve parameterization and make it evolve according to the MCF equations. But that requires computing the normal vectors and mean curvatures at each point of the curve, which is a bit trickier (it’s 100% doable in G’MIC anyway)

I may try to do this later if I have some time, but I don’t promise anything :slight_smile:

1 Like
22

anim_morph

foo :
  shape_dragon 420 # Source shape
  shape_heart 420 # Target shape
  ge 50% r 512,512,1,1,0,0,0.5,0.5

  # Extract contour parameterizations of largest components.
  foreach { edgels -1 k[{argmax(${"-lof h"})}] channels. 0,1 f. "I==J[-1]?[-1,-1]:I" discard. -1 r. 1,50%,1,2,-1 }
  r 1,${-max_h},1,2,1 1,32,1,1,y%2 r. 1,{-2,h} a[-3,-2] .,c rm.
  => source,target
  512,512,1,3,"lerp([0,0,0],[0,32,128],y/h)" => background
  (0^0^0^0,255^255^255^255,255^0^0^255) => colormap

  # Perform curve interpolation.
  repeat 200 {
    +j[source] [target],0,0,0,0,{cut(lerp(-0.25,1.25,$%),0,1)}
    {background,[w,h]} eval.. "pP = J[-1,2]; polygon(#-1,2,pP[0],pP[1],i0,i1,1,i2?2:1)"
    dilate. 3 map. [colormap] +ja[background] .
    w.
    on. frame.jpg,$>
    k[source,target,background,colormap]
  }
1 Like
24

A last one that combines linear interpolation and curvature-based evolution.
I like this one very much, the code is quite short. And it works for interpolating any complex shapes together!

anim

foo :
  shape_dragonfly 480 # Source shape
  shape_snowflake 480 # Target shape
  ge 50% r 512,512,1,1,0,0,0.5,0.5

  # Extract contour parameterizations of largest components.
  foreach { edgels -1 k[{argmax(${"-lof h"})}] channels. 0,1 f. "I==J[-1]?[-1,-1]:I" discard. -1 r. 1,50%,1,2,-1 }
  r 1,${-max_h},1,2,1 1,32,1,1,y%4 r. 1,{-2,h} a[-3,-2] .,c rm.
  => source,target
  512,512,1,3,"lerp([0,0,0],[0,32,128],y/h)" => background
  (0^0^0^0,255^255^255^255,255^0^0^255,255^128^0^255,255^255^0^255) => colormap

  # Perform curve interpolation.
  repeat 50 {
    k:=cut(lerp(-0.15,1.15,$%),0,1)
    [source] sh. 0,1 b. y,{lerp(0,100,$k)},2 rm.
    [target] sh. 0,1 b. y,{lerp(100,0,$k)},2 rm.
    j.. .,0,0,0,0,$k rm.
    {background,[w,h]} eval.. "pP = J[-1,2]; polygon(#-1,2,pP[0],pP[1],i0,i1,1,i2 + 1)"
    dilate. 3 map. [colormap] +ja[background] .
    w.
    rm[-3,-2]
  }
  rm[source,target,background,colormap]
2 Likes