A last one that combines linear interpolation and curvature-based evolution.
I like this one very much, the code is quite short. And it works for interpolating any complex shapes together!
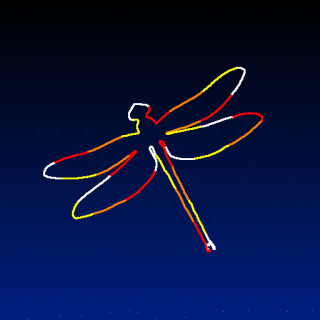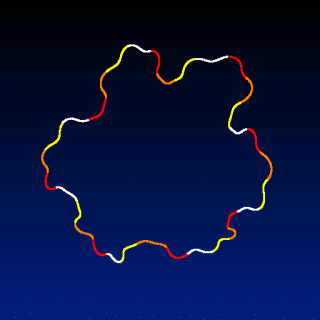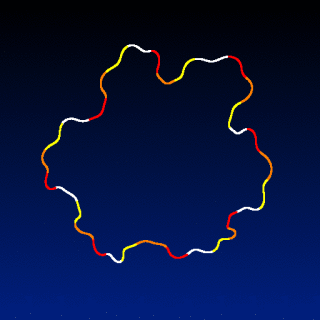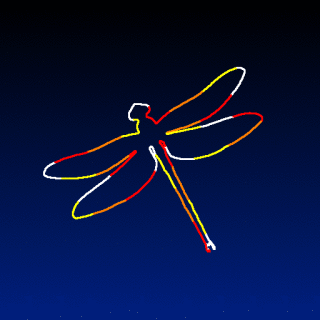
foo :
shape_dragonfly 480 # Source shape
shape_snowflake 480 # Target shape
ge 50% r 512,512,1,1,0,0,0.5,0.5
# Extract contour parameterizations of largest components.
foreach { edgels -1 k[{argmax(${"-lof h"})}] channels. 0,1 f. "I==J[-1]?[-1,-1]:I" discard. -1 r. 1,50%,1,2,-1 }
r 1,${-max_h},1,2,1 1,32,1,1,y%4 r. 1,{-2,h} a[-3,-2] .,c rm.
=> source,target
512,512,1,3,"lerp([0,0,0],[0,32,128],y/h)" => background
(0^0^0^0,255^255^255^255,255^0^0^255,255^128^0^255,255^255^0^255) => colormap
# Perform curve interpolation.
repeat 50 {
k:=cut(lerp(-0.15,1.15,$%),0,1)
[source] sh. 0,1 b. y,{lerp(0,100,$k)},2 rm.
[target] sh. 0,1 b. y,{lerp(100,0,$k)},2 rm.
j.. .,0,0,0,0,$k rm.
{background,[w,h]} eval.. "pP = J[-1,2]; polygon(#-1,2,pP[0],pP[1],i0,i1,1,i2 + 1)"
dilate. 3 map. [colormap] +ja[background] .
w.
rm[-3,-2]
}
rm[source,target,background,colormap]