Agx terminology (UI)

[s7habo (Boris Hajdukovic)]

@kofa

Still, the decisive fix seems to be the blue unrotation. And that’s actually applied in reverse (since it’s unrotation).

Yes.

The idea here is to leave the input primaries as they are because they are primarily used for “hue correction”and the transition to white. In this case, this amplifies the color shift towards yellow in green grass caused by sunlight, which already existed from the beginning.

This useful option of being able to adjust the primaries after the curve comes in handy here.

We could have corrected the color tone of the yellow grass towards green using input primaries by simply shifting the blue primary towards magenta:

However, by keeping blender-like preset in input primaries and reversing everything in output primaries (after the curve), we have the option of additionally correcting the color of the grass without losing the contrast and hue adjustments we gained through attenuation and rotation of input primaries.

[s7habo (Boris Hajdukovic)]

@kofa

I’ll have to check this in detail. Anything going black via rotation is… well, unintuitive.

When we rotate red towards yellow, green becomes darker and magenta becomes lighter:

At a certain point, green becomes black and magenta becomes white:

This is the same as if we set the green channel to zero and increase the green in the red channel instead. So, we mix red and green (red and green become yellow) and effectively have no green channel left:

[Christian_Pfister]

Channel mixing is… well unituitive
I always have to think twice, trice… how it works and what to do to achieve something specific.
Fortunately we have Boris who masters this brilliantly and teaches us patiently.

[kofa (István Kovács)]

That’s all nice and well, but my brain cannot understand why that happens. I see what happens, just not why, and that’s bugging me. Our brains work differently (some days, mine hardly works at all…).

[Christian_Pfister]

I don’t know whether rotation uses a specific formula but the channel mixer formula is rather simple:

Red(new) = R(input) x Factor(red) + G(input) x Factor(g) + B(input) x Factor(b)

What Boris did above, he took the green output channel, reduced G(input) to zero (therefore green goes to black) and and increased Input Red to 100%.

This means that wherever you have positive Red values, green is added at 100%. Thus Red turns to yellow. Where you also have blue, you get white (all 3 are at 100%).

It is as if he turned/rotated the Green circle up fully into the red circle.

[europlatus]

@Christian_Pfister

the channel mixer formula is rather simple:

It looks simple, but in 25 years, I still can’t predict what is going to happen when I mix channels. If I sit and work it out, maybe make a few diagrams or look at a few past examples, I can get a good idea. But that takes time, and more often than not I just find trial and error to be the quickest solution.
That bugs me, and so I avoid channel mixing whenever I can

[kofa (István Kovács)]

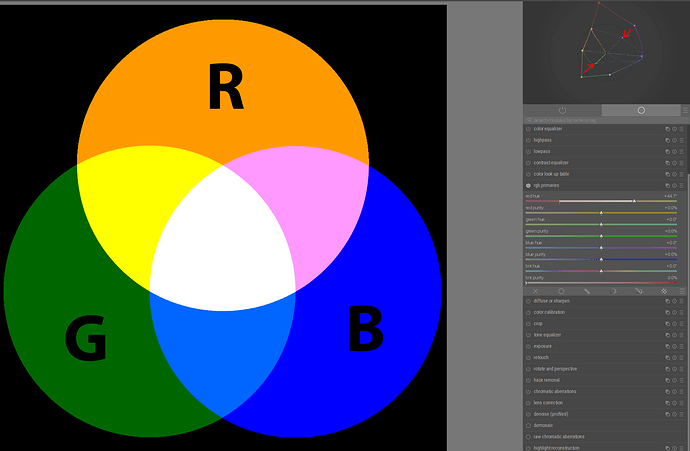
When we rotate and scale those primaries, what happens is, we create a new colour space, an reinterpret the meanings (the actual colours) of the RGB values according to it.

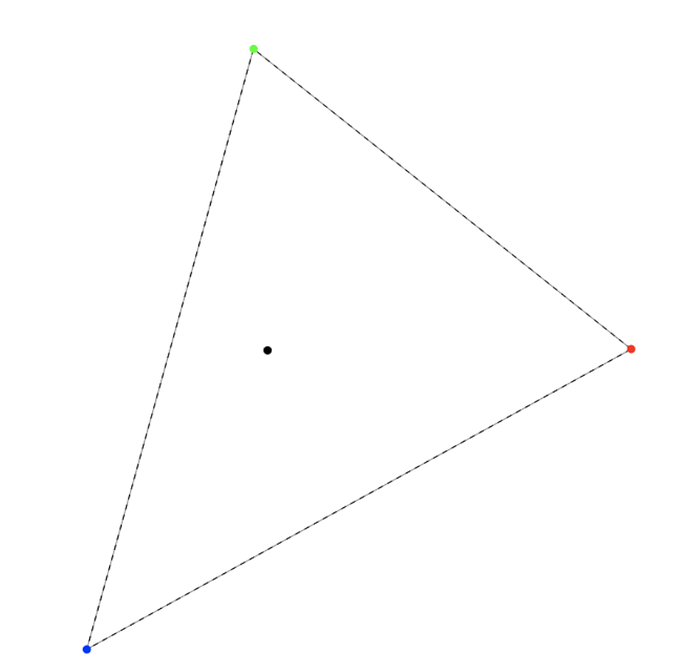
Below, the red, green and blue dots represent the rotated primaries. They reflect the hue, but not the luminance. This will be important in the case of our poor green primary.

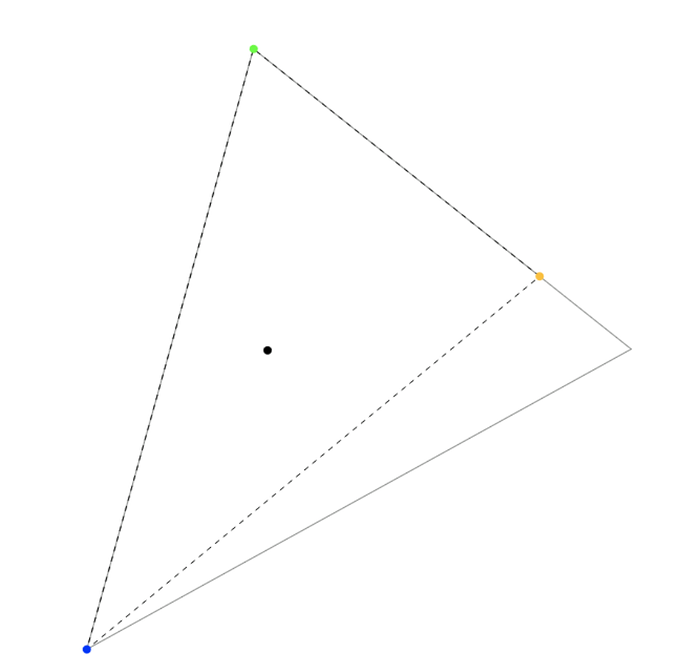
No rotations, no insets, starting from Rec 709:

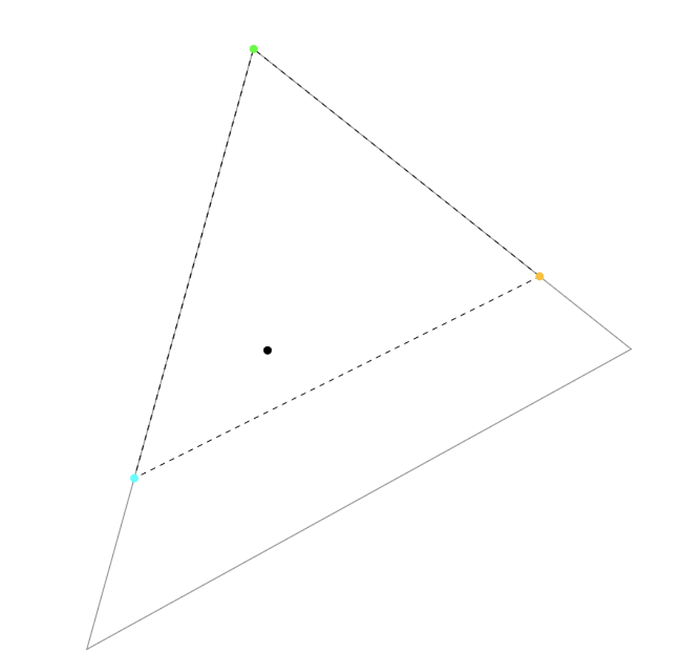
15° rotation of red:

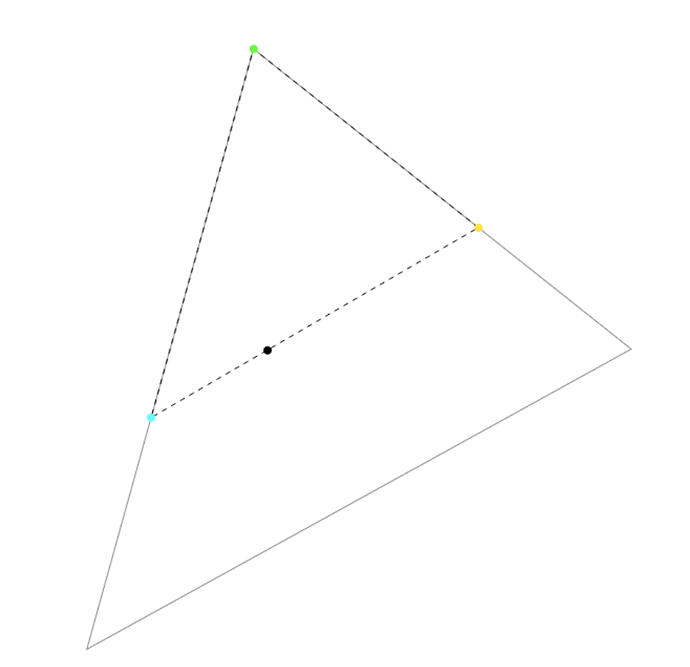
And then -15% of blue:

We are pushing the red - blue side closer to the achromatic. The white point has the xy coordinates of the achromatic, and a fixed luminance, Y = 1 (that’s why it’s the white point).
As the relative distances change, the significance of red and blue grows; that of green diminishes. The Y coordinates (luminances) of the original red, green and blue primaries are 0.2126, 0.7152, 0.0722; green is the brightest primary, by far, almost 10 times as bright as blue.

By the time we rotated the red by 15° and the blue by -15°, the Y values have changed drastically: 0.336286, 0.303979, 0.359735 - now blue is the brightest.
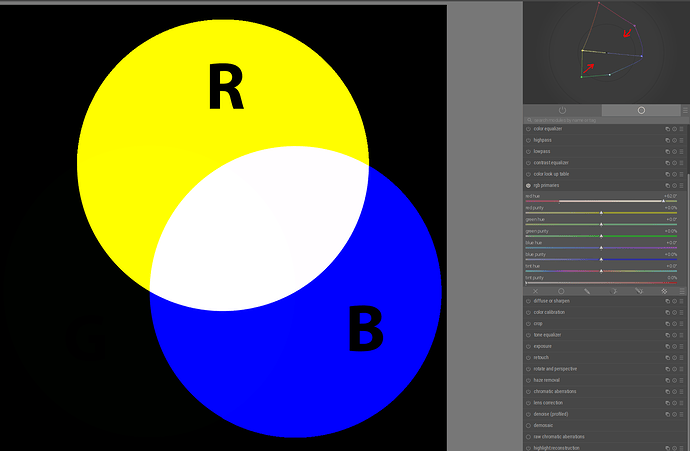
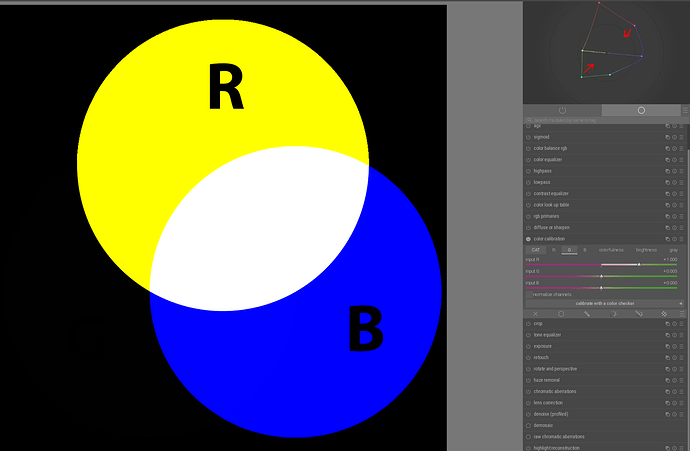
As we keep pushing red to 30°, and also blue towards -30°, there comes a point (at about blue = -28.8°) when the red - blue line crosses the achromatic:

We reached the point where ‘red’ + ‘blue’ (that is, yellow and cyan) add up to white. The Y coordinates are about [0.4758, 0, 0.5242] - green is basically black, it has no luminance left. And rotating blue further actually creates a space that cannot represent neutrals, as the white point’s chromaticity coordinates are out of gamut for that space. This is fun.

At least now I understand why green turns black. The rest, the ‘intuitive’ part, I still don’t get.

[kofa (István Kovács)]

Now for something completely different (we’ve shifted a bit from UI and terminology): my PR for the power → brightness and offset → lift change has been merged (thanks, @Pascal_Obry). It will perform a DB migration to convert the power to brightness in history stacks and presets.

The scene-referred default and the blender-like presets partially restore purity, as before, and they don’t restore rotations, as before. However, how they don’t restore rotations has changed. Previously the master rotation reversal slider was at 100%, and the individual red / green / blue rotation sliders were set to 0. Instead, now we set the master rotation reversal to 0, but set the red / green / blue rotation reversal sliders to the same values as the rotations. The net effect, as you start out, is the same; however, if you want to gradually restore rotations, you can do it using a single slider. The individual sliders are still available for further tweaks.

Finally, the least important change, out of pure pedantry: the built-in blender-like presets have changed a tiny bit (this does not affect the other presets, like scene-referred default, smooth and unmodified primaries): Blender uses gamma 2.4 by default, not 2.2 (my mistake). On the UI, you’ll see the contrast also updated to 2.45. Now, Blender uses a contrast of 2.4, but our contrast compensation logic rescales contrast using gamma 2.2 as a base, and after that, you’ll get a curve that matches Blender’s exactly (I’ve tested that by running a test with code from the original Python script). Anyway, internal maths stuff, not that interesting, I just wanted to let you know that it’s intentional. Of course you can continue to use whatever gamma and contrast you want, Blender is just provided as an example (the scene-referred default uses gamma = 2.2 and contrast 2.8, for example).

[siamak]

@Christian_Pfister

Fortunately we have Boris who masters this brilliantly and teaches us patiently.

@s7habo Boris are you listening? We need more videos. Please

[RawConvert (Andrew)]

@Popanz , I wouldn’t say the shift is huge, it seems mild to me. What I notice most is more local contrast in the grass in the first pic.

[kofa (István Kovács)]

Adding colour indicators to the primaries sliders (this has been requested): if I do this, how should the rotation sliders look?
The pre-curve controls are simpler, they could be like those in rgb primaries:

Those are quite fancy, BTW, as the purity sliders reflect the hue. For example:

However, the rotation reversal sliders are interesting.
There is reason to say they should look exactly like the rotation sliders, with the hue directions not flipped. Since these are reversal sliders, they would show what input hue you map to the selected primary. Internally, with the same pre- and post-curve settings, the two operations use the same matrix, only that the 2nd one is inverted: one undoes the effect of the other.

But I have the nagging feeling that people would want them the other way, e.g. if they shifted blue towards green, and got cyan they want to get rid of, they’d say “let’s shift blue towards red (magenta) this time” (and not “let’s shift cyan towards blue”). What do you think?

[Christian_Pfister]

Actually I don’t really care as long as it’s visible where to you go. But my first thought was to have the outset opposite to the inset, i.e. you first rotate in one direction and you reverse it in the other. I think this is your first option (no nagging feeling).

Edit: Sorry my ‘first thought’ was actually the ‘nagging feeling’ (2nd option). But I see your point with ‘reversal’ and reversing the signs. So I’m in favor of the first option.

[kofa (István Kovács)]

The first option above is using the same colours and also using the same direction. So, if you used -3.6° of blue rotation to turn your blues slightly cyan, you’d also use -3.6°; for both the before tone mapping and after tone mapping slider, cyan would be on the left, magenta on the right.

Reversing the sign is also an option, though, since the slider already say reversal, it would be confusing, I think, that a 29.46% red attenuation is reversed using an identical red purity boost, but a 2° red rotation is reversed using a -2° red rotation reversal. I would really, absolutely hate to reverse the sign.

And, I’d also keep the sliders coloured the same way: by selecting the cyan on the blue rotation reversal slider, you are indicating that you want to turn that hue blue. I know people will probably dislike that idea.

@Christian_Pfister

I don’t really care as long as it’s visible where to you go

That’s exactly my point: for the reversal slider, I would prefer to show where you come (back) from.

[europlatus]

@kofa

That’s exactly my point: for the reversal slider, I would prefer to show where you come (back) from.

If I’ve understood correctly, then the above would be the logical option for me too. This seems to be similar to how RGB Primaries works (fancy) in that the slider colours reflect the changes you’ve already made. In other words, they are somewhat contextual and help guide you to the desired result from your current starting point.

Did I understand correctly?

[siamak]

@europlatus

help guide you to the desired result from your current starting point.

I agree too. That is how it should reflect and behave. As you said it is also consistent with RGB Primaries.

[siamak]

I hope you do not think that I am nitpicking.
While at it, I am not sure if it has been brought up before, to me it seems more initiative to have the “toe power” slider below the “shoulder power” slider in the "basic curve parameters . The order of sliders in “advanced curve parameters” from top to bottom, target white, shoulder start, target black, and toe start or targets together and starts together such as target white, target black, shoulder start, toe start.

[priort (Todd Prior)]

I have thought about it and picked both at one point…the problem might be for the first one is that if you are matching it is sensible…so you shift to orange and then the same reversal in the postTM, reversing the same amount of orange for argument sake. But, I can see if the person just looks at this and moves the slider towards magenta and the image gets more orange or yellow then will the logic still be so obvious? Whereas, when the colors are inverted you have to think about the opponent slider but its doing what what the color says by shifting the image to match the color… I could get used to both but I have a bit of a feel for this module … what will be the feedback… it will be interesting to see how each is perceived.

I went intially to option 2 then I thought no option 1, but the more I kept thinking I thought maybe this was based just on this set of sliders what if someone was to move the slider to a different value and the opposite direct in the post tone mapping how would they behave and would it make sense and then I went more towards option 2 again…this is tricky…

[s7habo (Boris Hajdukovic)]

As far as I’m concerned, both options are fine, but they must remain consistent.

If you have “desaturated” something (attenuation), you add the saturation back (boost purity). This is indicated in both examples.

If you rotate a primary in one direction, reversal should rotate the primary back in the opposite direction. So, the color of the sliders should reflect this direction. And that is shown in the second example.

That is “reversal” from a logical point of view.

If you don’t want to violate this logic, in the first option, purity boost would have to run from right to left. So to speak, as “attenuation reversal.”

The reversal would then be recognized as a mirroring of the values of the input sliders.

[kofa (István Kovács)]

@s7habo

If you rotate a primary in one direction, reversal should rotate the primary back in the opposite direction

The primary you are rotating is not the primary you started with. It’s now a bit cyan, or magenta, or yellow. That’s how you end up at the original position.

The fancy looks are pretty, but not that important, Iv think: one is looking at the image to check colours, not at the sliders.

I’m really worried that we ‘agree’ on something, I implement it, but then it turns out no one understood correctly what the other is saying, and people will remain dissatisfied.

[Macchiato17 (Lars Fiedler)]

Still “+1” from my side.

@Macchiato17

I have a small suggestion regarding the order of the two sliders: As the toe influences the bottom of the curve and shoulder its top, I would like to suggest exchanging the sliders:

I think it somehow got lost, as there is so much great discussion and improvements ongoing. Thanks for lifting this up again, as I wanted to ask about it today

And thanks again to @kofa for caring also about all the user experience inputs and tons of things here and there. Appreciate it so much.